Ejercicios De Distribucion Normal Estandar Y Area Bajo La Curva

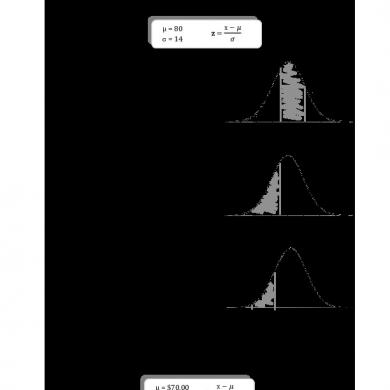
EJERCICIOS DE DISTRIBUCIÓN DE PROBABILIDAD NORMAL ESTÁNDAR 1. Una población normal tiene una media de 80 una desviación estándar de 14.0 x 𝜇 µ = 80 z 𝜎 σ = 14 a) Calcule la probabilidad de un valor localizado entre 75.0 y 90.0 p (75 ≤ x ≤ 90) Probabilidad acumulada.

z

=

z

= 0.3594

0.7611

75 80 μ

p (75 ≤ x ≤ 90) = 0.7611 – 0.3594 = 0.4017

90

b) Calcule la probabilidad de un valor de 75.0 ó menor. p(x ≤ 75) Probabilidad acumulada.

z

0.3594 p(x ≤ 75) = 0.3594 75 80 μ

c) Calcule la probabilidad de un valor localizado entre 55.0 y 70.0 p (55 ≤ x ≤ 70) Probabilidad acumulada.

z

= 0.2389

z

= 0.0367

p (55 ≤ x ≤ 70) = 0.2389 – 0.0367= 0.2022

55

70

80 μ

2. Los montos de dinero que se piden en las solicitudes de préstamos en Down River Federal Savings tiene una distribución normal, una media de $70,000 y una desviación estándar de $20,000. Esta mañana se recibió una solicitud de préstamo. ¿Cuál es la probabilidad de que: µ = $70,00 σ = $20,00

z

x

𝜇 𝜎

EJERCICIOS DE DISTRIBUCIÓN DE PROBABILIDAD NORMAL ESTÁNDAR a) El monto solicitado sea de $80,000 o superior p(x ≥ 80,000) z

Probabilidad acumulada.

–

= 0.6915

p(x ≥ 80,000) = 1 – 0.6915= 0.3085

70000 80000 μ

b) El monto solicitado oscile entre $65,000 y $80,000 p (65,000 ≤ x ≤ 80,000) z z

Probabilidad acumulada.

–

= 0.6915

–

= 0.4013

p (65,000 ≤ x ≤ 80,000) = 0.6915 – 0.4013 = 0.2902

65000 70000 80000 μ

c) El monto solicitado sea de $65,000 o superior. p(x ≥ 65,000) z

Probabilidad acumulada.

–

= 0.4013

p(x ≥ 65,000) = 1 –0.4013 = 0.5987 65000 70000 μ

3. Entre las ciudades de Estados Unidos con una población de más de 250,000 habitantes, la media del tiempo de viaje de ida al trabajo es de 24.3 minutos. El tiempo de viaje más largo pertenece a la ciudad de Nueva York, donde el tiempo medio es de 38.3 minutos. Suponga que la distribución de los tiempos de viaje en la ciudad de Nueva York tiene una distribución de probabilidad normal y la desviación estándar es de 7.5 minutos. µ = 38.3 min. z σ = 7.5 min.

x

𝜇 𝜎

EJERCICIOS DE DISTRIBUCIÓN DE PROBABILIDAD NORMAL ESTÁNDAR a) ¿Qué porcentaje de viajes en la ciudad de Nueva York consumen menos de 30 minutos? p(x ≤ 30) z

–

=

Probabilidad acumulada.

0.1335

p(x ≤ 30) = 0.1335 = 13.35%

30

38.3 μ

b) ¿Qué porcentaje de viajes consumen entre 30 y 35 minutos? p (30 ≤ x ≤ 35) z z

–

=

–

=

Probabilidad acumulada.

0.3300 0.1335

30

35

38.3 μ

p(30 ≤ x ≤ 35) = 0.3300 – 0.1335 = 0.1965 = 19.65% c) ¿Qué porcentaje de viajes consumen entre 30 y 40 minutos? p (30 ≤ x ≤ 40) z z

–

=

–

Probabilidad acumulada.

0.5910

= 0.1335 30

p (30 ≤ x ≤ 40) = 0.5910 – 0.1335 = 0.4575 = 45.75%

38.3 μ

4. Una distribución normal tiene una media de 80 y una desviación estándar de 14. Determine el valor por encima del cual se presentará 80% de las observaciones. µ = 80 σ = 14

z Probabilidad acumulada.

80% =

.8000

x

𝜇 𝜎

EJERCICIOS DE DISTRIBUCIÓN DE PROBABILIDAD NORMAL ESTÁNDAR En este ejemplo ya no se tiene que calcular la probabilidad (área) entre valores dados de x, sino que se tiene que calcular el o los valores de x a partir de porcentajes ó probabilidades que representan el valor de z. Y para encontrar el valor de x, tenemos que sustituir el valor de z en la formula y después despejar x. Al conocerse el porcentaje del cual queremos 80% ó 0.8000 obtener un valor x, en este caso 80%, se debe tomar en cuenta que este 80% también representa una probabilidad de .8000, esta probabilidad se la vamos a restar a 1 porque lo que queremos saber es a partir de qué valor de x X empieza ese 80% de observaciones, es decir por encima de ese valor. Entonces tenemos que: 1 – 0.8000 = 0.2000. Este resultado que también es una probabilidad 20% ó 0.2000 la tenemos que localizar en una tabla de probabilidades acumuladas de la distribución normal estándar, y así encontraremos el valor z que le corresponde, al ubicar este valor lo X podemos sustituir en la formula y encontrar x. a) Buscar en la tabla de probabilidades de la distribución normal estándar, el valor de z que tenga la probabilidad .2000 o la probabilidad que más se le acerque a esta. z

0.00

0.01

0.02

0.03

0.04

0.05

0.06

… …

… …

… …

… …

… …

… …

… …

… …

− 0.9 − 0.8 − 0.7 − 0.6 − 0.5

0.1841 0.2119 0.2420 0.2743 0.3085

0.1814 0.2090 0.2389 0.2709 0.3050

0.1788 0.2061 0.2358 0.2676 0.3015

0.1762 0.2033 0.2327 0.2643 0.2981

0.1736 0.2005 0.2296 0.2611 0.2946

0.1711 0.1977 0.2266 0.2578 0.2912

0.1685 0.1949 0.2236 0.2546 0.2877

…

…

…

…

…

…

…

…

b) El valor de z que corresponde a esta probabilidad es -0.84. c) Ahora ya se puede sustituir z en la formula y encontrar el valor de x. x x 𝜇 -0.84 z 𝜎 -0.84 14 = x – 80 -11.76 = x – 80 -11.76 + 80 = x x = 68.24 X= 68.24

EJERCICIOS DE DISTRIBUCIÓN DE PROBABILIDAD NORMAL ESTÁNDAR 5. Las ventas mensuales de silenciadores en el área de Richmond, Virginia, tiene una distribución normal, con una media de $1,200 y una desviación estándar de $225. Al fabricante le gustaría establecer niveles de inventario de manera que solo haya 5% de probabilidad de que se agoten las existencias. ¿Dónde se deben establecer los niveles de inventario? µ = 1,200 σ = 225

x

z

𝜇 𝜎

Probabilidad acumulada.

5% =

1 - 0.0500 = 0.9500 Valor z = 1.65 z

x

𝜇 𝜎

1.65

.0500

x–

5% ó 0.0500

X= 1,571.25

x = 1571.25

6. En 2004 y 2005, el costo medio anual para asistir a una universidad privada en Estados Unidos era de $20,082. Suponga que la distribución de los costos anuales se rigen por una distribución de probabilidad normal y que la desviación estándar es de $4,500. El 95% de los estudiantes de universidades privadas paga menos de ¿Qué cantidad? µ = 20,082 σ = 4,500

z

Probabilidad acumulada.

95% = z

x

𝜇 𝜎

x = 27,462.

1.64

.9500 x–

x

𝜇 𝜎

Valor de z

= 95% ó 0.9500

X= 27,462 75

EJERCICIOS DE DISTRIBUCIÓN DE PROBABILIDAD NORMAL ESTÁNDAR 7. El fabricante de una impresora láser informa que la cantidad media de páginas que imprime un cartucho antes de reemplazarlo es de 12,200. La distribución de páginas impresas por cartucho se aproxima a la distribución de probabilidad normal y la desviación estándar es de 820 páginas. El fabricante desea proporcionar lineamientos a los posibles clientes sobre el tiempo que deben esperar que les dure un cartucho. ¿Cuántas páginas debe indicar el fabricante por cartucho si desea obtener 99% de certeza en todo momento?

µ = 12,200 σ = 820 99% = 1 -0.99 = Valor z = - 2.33 x 𝜇 z 𝜎

z

x

𝜇 𝜎

Probabilidad acumulada.

.9900

0.01 99% ó 0.9900

- 2.33

x = 10,289.4

x–

X= 14,110.6

BIBLIOGRAFÍA

Lind, D. A., W. G. Marchal, y S. A. Wathen. (2008). Estadística aplicada a los negocios y a la economía. (13a Ed). México: McGraw-Hill. 239 - 242.